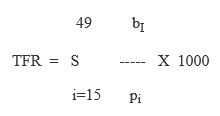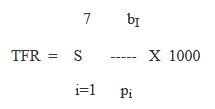Demographic Aspects of Educational Planning
N. K. Mohanty
Assistant Professor
Department of Educational Planning
NUEPA, 17-B, Sri Aurobindo Marg, New Delhi- 110016, India
Introduction
Education is for people and its development is ultimately aimed at maximizing the capacity for achieving full welfare of the population. The educational planner as well as administrator is constantly engaged in activities for and with the people.
The question arises: What are the demographic challenges facing educational planning today? It is vital for planners and decision-makers to know the structure and distribution of the population at a given date, as well as how it has changed in recent years. In other words, educational planning cannot be divorced from considerations about dynamics of population (i.e., its growth and change), as it deals with a ‘target population’ which is constantly changing in number, age and sex composition, and geographic distribution.
Population growth results in significant variations in the age and sex compositions of the population besides the numerical increase. The rate of population growth has wide implications on all spheres of human activity. Migration of people determines their geographical distribution and this too, has a significant impact on the needs of the society.
All these affect educational development in a direct manner. In fact, the findings of demography are one of the foundations on which educational plans are built and for this reason, planners should have a sufficient knowledge of demographic methods and concepts, their meanings and limitations. Nearly all quantitative analyses and estimates of the qualitative aspects of education are related to population – its size, structure, location, dynamics and prospects. Hence there is need to study demographic aspects of educational planning.
The discipline of the study of human population is known by two terms: (i) population studies (ii) Demography. Population Studies can easily be understood as studies concerned with population. Demography has been derived from the latin word ‘demos’, meaning people and hence is the science of population. Demographic analysis is confined to a study of the components of population variation and change. Population studies are concerned not only with population variables but also with the relationships between population changes and other variables – social, economic, political, biological, genetic and geographical etc.
Whereas the theoretical demographic analysis tries to explain demographic facts and to seek the causes behind them, the descriptive approach limits oneself to a ‘statistical description of populations’. In reality, however, the distinction is not as clear as this; population forecasts, for instance, cannot be made without a minimum of demographic analysis.
Whichever approach is adopted, demographers have two possible fields of study distinct from each other, both in objectives and in method. The first one is static demographic analysis which deals with the current situation of the population, their structure or composition. The second one is the dynamic aspect of population analysis which aims at the trend of the population – also called movement of the population which depend on a number of factors, particularly on such demographic events as births, marriages and deaths.
Section I of this paper deals with the structure of a population and its effects on educational problems, and Section II deals with population trends or movements and their impact on educational planning over the longer term.
I. Population Structure and Its Effects on Education
Studying the structure of a population means studying its composition, i.e., its distribution according to certain pre-defined criteria. Educational planners may be concerned with the distribution of the population for various reasons.
First, they may be interested in its distribution by age and sex. This enables them to measure the relative size of the school-age population, which is the foundation and the point of departure for any educational policy.
Second, they may be concerned with the distribution of the population by sector of economic activity and, within each of these sectors, by occupation. Without accurate knowledge of the distribution by sector and occupation, it is impossible to estimate manpower requirements, and hence to determine targets for technical, vocational and higher education.
Third, planners may be concerned with the geographical distribution of the population, which affects both the cost of education and the choice of types, sizes and locations of schools. Our examination of population structure will be confined to the three above-mentioned aspects.
Structure of the Population by Age and Sex
The simplest method of studying the population structure by age and by sex is to construct an ‘age pyramid’. The age structure of the population is very important in demographic analysis because it provides a sort of summary of the demographic history of the nation, and also because, as it governs to some extent the future growth of the population.
The number of individuals at each age, or in each age group, depends on (i) the number of births in the generation, or generations, of which they were born; (ii) the effect of mortality on that generation or those generations; and (iii) the size of migratory flows at various times, and the ages of the migrants.
Age Composition
The age structure of a population is the consequence of trends in fertility (birth), mortality (deaths) and migration over past periods with fertility trends having the dominant influence. The proportion of small children, for instance, reflects the recent birth rate as further affected by infant mortality.
The proportion of old person is a cumulative effect of population trends ever since the time when they are born. The population of children aged 0-4 years gives an indication of the burden of child care. The group 5-14 is an indicative of investment needed for school enrolment and teaching staff. The economically active population is reflected by the 15-64 group while a rough index of old age dependency is the proportion of the population aged 60 years and over.
Dependency Ratio
The size of the age-group 15-64 years in relation to the rest of the population in the two age-groups, 0-14 and 65 years and above provides an idea about the magnitude of the burden of dependency on it. The estimation of the extent of economic dependence in a population is the main use of working out the dependency ratio.
Total Dependency Ratio = Young Dependency Ratio + Old Dependency Ratio
More generally, whenever the birth rate falls for one reason or another, this decrease will affect the number of children in primary education six years later, the number in secondary school 12 years later and the number in higher education 18 years later.
This has occurred in some Asian countries, such as the Republic of Korea, China and Thailand, and such Latin American countries as Chile and Costa Rica. Such a trend makes it easier to absorb the increased social demand for secondary and higher education.
The structure of the population by age can also yield much other useful information for educational planning. It can be used, in particular, to measure the relative burden of expenditures on education. Expenditures on education are proportionate to enrolment and consequently depend indirectly on the school-age population, but the financing of education can be considered as a levy on the output of the economically active part of the population.
If the school-age population is made up of children from 5 to 14 years of age inclusive, and the active population is recruited from persons aged 15 to 64, an estimate of the relative burden of educational expenditures on the active population is obtained by calculating the ratio of the 5 to 14-year-old population to the 15 to 64-year-old population. This proportion varies widely from one country or region of the world to the next, as shown in Table 1.
Table 1. School-age population and working-age population (in thousands), 1995
| Age group | Age group | ||||||||||
| Country | 5-14 | 15-64 | (1)/(2) | Country | 5-14 | 15-64 | (1)/(2) | ||||
| (1) | (2) | % | (1) | (2) | % | ||||||
| Sub-Saharan Africa | Latin America | ||||||||||
| Mauritius | 198 | 742 | 26.7% | Chile | 2,714 | 9,094 | 29.8% | ||||
| South Africa | 8,693 | 22,669 | 38.3% | Argentina | 6,641 | 21,452 | 31.0% | ||||
| Senegal | 2,282 | 4,548 | 50.2% | Brazil | 34,419 | 101,185 | 34.0% | ||||
| Cameroon | 3,572 | 6,881 | 51.9% | Colombia | 8,518 | 23,549 | 36.2% | ||||
| Zimbabwe | 3,044 | 5,849 | 52.0% | Jamaica | 539 | 1,471 | 36.6% | ||||
| Nigeria | 27,311 | 51,950 | 52.6% | Mexico | 21,146 | 54,869 | 38.5% | ||||
| Congo | 702 | 1,301 | 53.9% | Costa Rica | 810 | 2,079 | 39.0% | ||||
| Kenya | 8,138 | 13,853 | 58.7% | Venezuela | 5,155 | 13,106 | 39.3% | ||||
| Arab countries | Industrialized countries | ||||||||||
| Syria | 2,084 | 5,411 | 38.5% | Japan | 14,053 | 87,078 | 16.1% | ||||
| Iraq | 6,154 | 15,787 | 39.0% | Germany | 9,146 | 55,774 | 16.4% | ||||
| Tunisia | 15,882 | 35,999 | 44.1% | Sweden | 1,056 | 5,606 | 18.8% | ||||
| Algeria | 7,155 | 16,049 | 44.6% | United Kingdom | 7,522 | 37,784 | 19.9% | ||||
| Morocco | 4,691 | 10,185 | 46.1% | Canada | 4,000 | 20,087 | 19.9% | ||||
| Egypt | 5,486 | 10,891 | 50.4% | France | 7,659 | 38,003 | 20.2% | ||||
| Saudi Arabia | 4,260 | 7,427 | 57.4% | Australia | 2,584 | 11,934 | 21.7% | ||||
| Asia | United States | 38,985 | 174,364 | 22.4% | |||||||
| Rep. of Korea | 7,102 | 31,869 | 22.3% | New Zealand | 562 | 2,401 | 23.4% | ||||
| China | 219,693 | 822,628 | 26.7% | Pakistan | 213,809 | 597,546 | 35.8% | ||||
| Thailand | 11,429 | 39,269 | 29.1% | ||||||||
Source: United Nations, 1999.
In Africa – with the exception of Mauritius, whose situation is somewhat exceptional, and South Africa – the ratio of children aged 5 to 14 to the active population exceeds 50 per cent. This means that, for purely demographic reasons, the goal of ‘education for all’ is much harder to achieve in Africa than elsewhere. The proportion is also very high in the Arab states, whereas in Asia the situation is more diversified. In the Republic of Korea it is only 22.3 per cent, whereas in the Philippines it amounts to 42.5 per cent, a level comparable to that of the African and Arab countries.
In Latin America, where the influence of the Catholic Church is still predominant, the situation lies between these two extremes, but with significant differences from one country to another, ranging from 29.8 per cent in Chile to 39.3 per cent in Venezuela. Lastly, this percentage is lowest in the countries that have long been industrialized. In Japan and Germany, it is only about 16 per cent. Educational development thus has two factors working in its favour in the wealthy countries: abundant resources, and a proportionally smaller school-age population.
Age Structure and School Enrolment Rates
As discussed earlier, the age structure enables to estimate the relative size of the school-age population. It also enables to calculate the school enrolment rates in order to try to answer the following question: ‘What proportion of children receive an education?’.
Although the answer to this question seems very clear, one cannot give an entirely satisfactory answer because two different indicators are recommended: the gross enrolment rate (GER), and the net enrolment rate (NER). The gross enrolment rate is calculated as the ratio of the total number enrolled at a given educational level to the age group corresponding to the official age at that level.
If, for example, primary education comprises five years of schooling and the official age of admission is six years, the gross enrolment rate in primary education is equal to: GER = (Total number of pupils in primary education/ Total 6 to 10-year-old population) * 100 This method of calculation leads to overestimation of school enrolment: Some children may be admitted early, before the official age; while others are over the official age, owing to either late admission or repetition of grades.
For this reason, a net enrolment rate is also calculated: NER = (No. of pupils in 6 to 10 years of age in primary education/ Total 6 to 10-year-old population) * 100. Unfortunately, the net enrolment rate has the opposite disadvantage as the gross rate: it underestimates enrolment rates, since all pupils above and below the official age range are excluded.
The enrolment rate for an entire educational level, whether gross or net, is thus not an entirely satisfactory indicator. For this reason, enrolment rates are also calculated for each year of age. The enrolment rate for 6-year-olds, for example, is equal to: ER 6 years = (No. of 6-year-old pupils in primary education/ Total 6-year-old population) * 100.
Enrolment rates by specific age are more precise than those by age group, but they do not fully dispel the ambiguity. A 6-year-old enrolment rate of less than 100 per cent does not mean that not all children are admitted to school. Some may enter school at 7 years of age, at 8, or even later still. In addition, at 12 years some children are still in primary education, while others have entered secondary school. Hence the question arises as to how should the enrolment rate for 12-year-olds be calculated, and most importantly, how should this indicator be interpreted?
It is possible that the question ‘What proportion of children receive an education?’ is not entirely appropriate, and that it would be better to split it into two questions: (i) What proportion of children are admitted to school?; (ii) What level do they reach? The first question has to do with access to education, while the second relates to the efficiency of the education system (from an economist’s point of view) or the quality of education (from an educator’s point of view).
(a) Measuring Access to Education
Access to education is first and foremost a question of school location3. How is provision of schooling organized? What is its geographical distribution? How far must children travel to attend school? This question of the physical accessibility of schooling is the principal issue, but it is not the only issue: There is also ‘economic’ accessibility (the costs to parents of sending their children to school) and ‘socio-cultural’ accessibility (parents’ attitudes regarding the need to send children to school) (Carron and Châu, 1981).
Access to education can be measured by the gross admission rate, or apparent admission rate, which is obtained as follows: Gross Admission Rate = (New admissions to primary education / Total 6-year-old population) * 100. The gross or apparent rate of admission has disadvantages similar to those of the gross enrolment rate. As a result of early or late admissions, it may exceed 100 per cent, with no assurance that all children have really been admitted to school.
A more appropriate means of measuring admissions is the cohort admission rate. This is obtained by monitoring a cohort of children born in the same year and counting how many are admitted to school successively at 5 years of age, then 6 years, then 7 years, etc. By following such a cohort, we obtain a more accurate view of real admissions and can ensure that we have arrived at a figure for total admissions. The admission rate for the cohort can never exceed 100 per cent , since the number of children in a cohort who have been admitted to school cannot be greater than the total number of children in the same cohort.
Obviously, no matter how great an effort is made to construct relevant and valid indicators (i.e. indicators corresponding to what one really wants to measure), the reliability of the indicator is still wholly dependent on that of the data used to calculate it.
(b) Measuring the Efficiency of the Education System
Having answered the question ‘What proportion of children are admitted to school?’, we now turn to the second question: ‘What level do they reach?’ To obtain a more precise answer, Johnstone (1982) suggests that this question be divided into three questions. He recommends three indicators that are intended to answer the following three questions: (i) How many years on average does a child spend in primary education?; (ii) What is the average grade he or she reaches within this educational level?; and (iii) What proportion of the pupils admitted to this educational level completes primary education?
The first indicator may be different from the second, since the average time spent in primary education may be greater than the grade reached, owing to repetitions. The third indicator is perhaps the most meaningful for measuring the efficiency of the education system, as it indicates the proportion of children who have successfully completed primary education. A fourth indicator may be added to the three mentioned above: the number of pupil-years of schooling that must be provided for one pupil to complete primary education.
Age Structure of Teachers and Cost of Teaching Staff
Age distribution analysis may of course be used in areas other than that of the school-age population. For example, it may be applied to the teaching force. As retirement is the major cause of the loss of teaching staff, accurate information on the age structure of the teaching force allows us to prepare for these losses. Another possible application of the age pyramid to the teaching force is concerned with salaries. Since teachers’ salaries are geared to levels of seniority, the structure of the teaching force by year of seniority enables us to forecast the financial effects of the shifts in pay grade that come with increasing seniority.
It is obvious that the average salary, and consequently the unit costs, are higher when the bulk of the teaching force is made up of comparatively old persons than when the majority of teachers are relatively young.
Population Structure by Economic Activity and Problems in Forecasting Manpower Requirements
The first question that arises is what proportion of the total population is economically active, or in other words, the distinction between the active population and the inactive population. The proportion of economically active persons varies according to age and sex. For this reason, it is useful to calculate by sex the percentage of the population counted as being economically active in each age group.
Distribution of the Population by Sector of Economic Activity
Economic activity is traditionally divided into three sectors: the primary sector, covering activities in which production is based on natural resources (agriculture, mining, etc.); the secondary sector, which consists of the manufacturing and processing industries; and the tertiary sector, made up of the service industries. The tertiary sector is the most heterogeneous. It includes all kinds of activities, but two of its sub-sectors merit special mention: the sub-sector of commerce in its broad sense (banking, insurance, transport and retailing), and the sub-sector of culture and recreation (education, radio, television, publishing, entertainment etc.).
The relative sizes of these three sectors have varied considerably over time. In the wealthy countries, it is currently the tertiary sector that predominates, although in Germany and Japan, the secondary sector has retained its importance as it employs over one-third of the active population. In the developing countries, substantial changes have occurred in sectoral structure since 1960. The share of the primary sector has diminished in all countries, but it remains the dominant sector in some African countries, such as Kenya and Zimbabwe, and in such Asian countries as India, China and Thailand.
The secondary sector has grown remarkably in the ‘newly industrialized’ countries such as Mauritius, Tunisia, the Republic of Korea and Argentina. The share of the tertiary sector has increased significantly in all countries.
In addition to the distribution of the population by sector of activity, educational planners need to know the distribution by occupation in order to forecast manpower requirements. In order to prepare forecasts of manpower requirements, it is often necessary – since all sectors of economic activity do not develop at the same pace – to make cross-classifications, giving, for example, the classification by occupation within each sector of economic activity.
If the expected increase in production in each sector of activity is known, the manpower requirements for the various occupations or types of employment can be estimated on the basis of this cross-classification. A difficult problem remains, however, in linking jobs to qualifications; that is, matching the occupation to the type of training received. In any event, no matter how many precautions are taken, any forecast of manpower requirements will only be an approximation (Harbison, 1967; Youdi and Hinchliffe, 1985; Bertrand, 1992).
Geographical Distribution of the Population and the Problem of Location of Educational Institutions
The distribution of the population over a country’s territory is far from uniform; some areas are densely populated, others much less so. Moreover, when there is no policy for balanced growth (such as a regional development plan), this difference may even increase: The population of already densely inhabited areas may continue to grow, while that of scarcely populated areas may diminish.
Measuring the Geographical Distribution of a Population
A first method of assessing the geographical distribution of a population is to conduct a study of the population density of different areas. In order for a survey of this kind to be meaningful and useful, it must be conducted at the level of the smallest geographical or administrative units, as an average density figure is of less significance.
In addition, the presence of a large town or city in a certain area automatically raises the population density of the administrative unit to which it belongs, and thereby distorts the data for the surrounding rural areas contained within that unit. For this reason, the population of urban centres is sometimes excluded from density calculations.
Another way of estimating the geographical distribution of the population is to classify administrative units by number of inhabitants. But here again there is a sizeable drawback, because the overall size of the population of such a unit provides no indication as to the local characteristics of human settlements within that unit (whether they be concentrated or dispersed). This is a problem because such data are the most important factor in planning the location of schools.
Planning the Location of Schools
Two considerations, which may sometimes be contradictory, must be taken into account when locating schools: the size of the local population, and the catchment areas of the school. Where population size is concerned, the issue is obvious: There must be a minimum number of pupils living in an area in order to justify the building or opening of a school.
This is particularly true for secondary schools, with their greater number of both compulsory and optional subjects. It is also important, however, that the area served should not be too large, so that the pupils can easily reach the school from their homes. The acceptable limits of that area depend on the ages of the children, the facilities provided (e.g. the existence of a school lunch room), the means of transport available (e.g. whether a school bus service is provided), the nature of the terrain (plains or mountainous areas) and the severity of the climate.
Of course, in densely populated areas, the size of the area served is no longer problematic; there is always a sufficient population so the area served by the school does not need to be very large. But the situation is different in more thinly populated areas, and especially in rural areas.
At the secondary level, because of the optional courses offered and the number of subjects to be taught, a greater number of students is needed to justify the creation of a school. Depending on the age distribution of the local population and the proportion of children attending school, the overall population size will vary considerably, and the catchment area for the secondary school may be very large. Of course, the provision of a school bus system or accommodation for boarding students could allow the catchment area to be extended, but such measures increase the cost.
In any event, it should be noted that the location of schools is not and cannot be based on purely theoretical considerations. Many factors have to be taken into account, and all these factors may vary from one area to another. It is the people at the local level who are more familiar with these factors, and that is why the local authorities should be as involved as possible in the school mapping process. Another problem that may arise relates to differences in enrolment rates from one area to another.
In such cases, it is up to the government to decide whether existing differences should be reduced, or whether – on the contrary – educational development should focus first on the areas where demand is strongest.
The problem of reducing regional disparities in access to education is highly complex, requiring not only a deliberate policy choice, but also additional resources: “The school system tends to develop more quickly in areas where it is already well established, rather than in disadvantaged areas … Moreover, the way in which demand is expressed and the strength it acquires also vary according to the economic, political and cultural situation of groups and according to the resources at their disposal for organizing themselves.
For this reason, an education policy that consists in satisfying demand on a first-come first-served basis as it is expressed by different groups tends to sharpen disparities rather than reduce them. To the contrary, reduction of disparities – which presupposes a rebalancing of educational development from area to area and a special effort in favour of disadvantaged areas – requires working against the spontaneous development of the system. It can therefore only be deliberate, and at the same time difficult to implement.” (Carron and Châu, 1981)
A further complication arises when different areas have different unit costs (due to lower pupil/teacher ratios and the necessity of paying salary bonuses to encourage teachers to take less desirable posts). Following the same line of thought, it must be noted that as the school enrolment rate increases, so does the number of problems regarding choosing school locations.
The objective of compulsory schooling implies the creation of schools in increasingly out-of-the-way places, with all the consequences this can have on costs. Planning the location of schools is still more complicated in multi-ethnic and multi-lingual countries, since it is necessary to take these special local characteristics into account (Hallak, 1977; Caillods, 1983).
II. Population Growth and Its Impact on Educational Planning
Section I focussed on the various aspects of population structure and their effects on education-related problems. But educational planners are not content with knowing the current situation; they are also interested in getting an accurate picture of the problems to be encountered in the future. In particular, they must know how the population will change in future years. This section will deal with the population changes and their impact on educational planning.
The population of any place at a specific time is a function of three types of events – births, deaths and migration and consequently, there are four ways in which the number of people of any area may change; (i) Children may be born in that area; (ii) The inhabitants of that area may die; (iii) People from other areas may move into that area (In-migration); and (iv) Inhabitants of that area may move out (out-migration).
These components of population change namely births, deaths and migration are identified as fertility, mortality and migration respectively and are known as demographic or population variables because the size, growth, structure and distribution of any population are determined by them. A study of any population is made through a study of these demographic variables. The change in population can be measured by (a) The difference between population sizes at different times (known as growth which results in either increase or decrease) (b) The analysis of the 4 components of population namely births, deaths, immigration & emigration.
Method of Measuring Growth Rate of Population
Simplest Approach (Growth Rate Method)
n
P = Po {1+ (r/100 )}
n
Po = Size of population at beginning of the period
P = Size of the population at the end of the period
n
n = Number of intermediary years
r = Average annual rate of growth
Crude Rate of Growth
The Crude Rate of Natural Increase (CRNI) permits the measurement of the change in population size per 1000 persons. This rate, generally expressed as a percentage of the total population, shows the balance of births and deaths and does not include the effect of migration.
B – D
C. R. N. I. = ——– X 1000
P
B = Number of births in a given year
D = Number of deaths in a given year
P = Mid-Year population corresponding to that year
Measures of Population Growth
The Simplest Measure is C.B.R. – C.D.R.
Number of Births in a Year
C.B.R. = ————————————- X 1000
Mid-Year population
Number of Deaths in a Year
C.D.R. = ————————————- X 1000
Mid-Year population
Rate of Natural Increase = C.B.R. – C.D.R.
Vital Index
Population growth as defined above is just an overall appreciation of the change in size. Crude rates (such as the CBR and CDR) are however, totally inadequate for the needs of educational planners hence the need for more refined measures of fertility and mortality so as to eliminate the effect of age structure.
In the following section, we shall first discuss methods of measuring natality before looking at some of the trends in natality in selected countries.
Methods of measuring natality
Fertility measures the rate at which a population adds itself by births. It is normally assessed by relating the number of births to the size of some sections of the population, viz. the number of married couple or the number of women of child-bearing age, i.e. an appropriate yard stick of potential fertility. Quite clearly in the consideration of fertility measures, the choice of the population at risk is important. Two types of rates are used to assess natality: the crude birth rate, and fertility rates.
The crude birth rate
No. of Births in a Year
C.B.R. = ——————————- X 1000
Mid Year Population
B
= ——————————- X 1000
P
This, the simplest rate, is calculated as the ratio of the number of live births during a year to the average population for that year. The average population for a year can be considered either as the population figure for 1 July of that year, or as the average of the population figures for the beginning and the end of the year. Although the crude birth rate has the advantage of being a simple rate, easily obtained from general data, it nevertheless has certain disadvantages. One of these disadvantages is that it gives the ratio of live births to the total population, whereas, in fact, only a part of the female population is capable of bearing children.
Consequently, the crude birth rate will vary with the structure of the population by age and sex, or more precisely the percentage of women of child-bearing age in relation to the total population. This rate, therefore, cannot be used to make comparisons between countries, because age structures may be very different in one country than in another. This is why demographers prefer to use fertility rates rather than the crude birth rate.
Fertility rates
The term ‘fertility’ is used to indicate the proportion between the number of births and the number of women of child-bearing age. A distinction can be made, however, between the general fertility rate and age-specific fertility rates.
General Fertility Rate (GFR)
This rate is the ratio of live births to the number of women of child-bearing age (considered by convention to be women of 15 to 49 years). As in the case of the crude birth rate, this rate is expressed per thousand.
Total Number of Live Births
In a given year
GFR = ————————————- X 1000
Mid-year female population
in the Reproductive
Or child-bearing Age-Group (15-49)
In the same year
B
= ——————————— X 1000
Pi
B = Total number of live births
Pi = Mid-year population of women between the ages of 15 and 44 or 49
Although GFR is a refinement over the CBR, it is not a very effective refinement because it is related to all the women in the child bearing group. But it is well known that fecundity, i.e., the psychological capacity to bear children during the child-bearing years is not uniformly distributed.
It has been observed that the rate of child-bearing is low in the younger age-groups (15-19), is the highest at ages between 20 and 29 when the majority are married and fecundity is at its maximum and then it tapers off till at the age of 50 it reaches the zero max. The fact that the fecundity of women is not the same during the entire span of the child-bearing period tends to be lost sight of, when the GFR is computed. For this reason, GFR is not considered to be a very effective refinement.
Age Specific Fertility Rates
Fertility Rate with respect to age is called ASFR. In this method, the reproductive span is divided into different sub-groups and fertility rate is worked out for each age-groups.
Bi
ASFR = ——- X 100
Pi
Where Bi = The number of live births born to women belonging to the age-groups during the year
f
Pi = Total number of women in the age-group
Merits and Demerits
ASFRs are not affected by any variations in age structure and therefore these rates may be considered to be refinement over GFR. It is also possible to compute age specific fertility rates with reference to only married women. These rates are then called age specific marital fertility rates and are even more refined than the ASFR because it is the married women who are exposed to the risk of child-bearing.
Despite the fact that age specific fertility rates provides a neat of six to seven rates for the different age-groups when comparisons between two population groups have to be made, the entire procedure becomes rather cumber some. Then the total Fertility Rate is applied.
Total Fertility Rate
The TFR is the sum of the age specific fertility rates of women in each five year age group from 15 to 44 or 49 during a particular time period.
Due to the unavailability of data this ratio is calculated on the basis of 5 years intervals (15-19, 20-24, ………., 44-49), while the birth rate for each 5 year group is an average for the group. There are 7 of these birth rates between ages 15-49 and so they are assumed from 1 to 7 as follows.
The above rate represents the number of children that would be born for each female in the age-group of 15-49.
Merits and Demerits
The TFR is a hypothetical rate indicating the total number of children that would even be born to a hypothetical group of women, if the group pass through its reproductive span of age. The TFR assumes that the women in this hypothetical cohort or group would survive till they reach the end of the reproductive period. As the TFR is not affected by the age-structure of the women under study, it is an effective summary rate for describing the frequency of child-bearing in a year. It is also useful when comparisons between the reproductive performances of two groups of women are made, for it is standardised for age and is just one summary measure.
However, where there is no deliberate birth control, fertility rates by age indicate the biological capability of women to bear children: the fertility rate is higher among young women and tends to fall as their age rises. In this case, it is possible to forecast the number of future births with some degree of accuracy on the basis of the age distribution of women and the fertility rate by age. Where birth control is practised, however, this rate becomes difficult to interpret.
When the size of the family is intentionally restricted and when the births are deliberately spaced, the age of women is no longer the only factor affecting fertility. Other factors come into play, such as age at marriage, length of time married, and the number of children preceding a given birth.
The number of births has great significance for educational planners, as this number determines the future number of pupils and students in the various levels of the education system. In most countries, educational planning is concerned with increases in the number of pupils and students, but in others – after a period of declining natality – it may involve planning for a drop in this number, a task that raises problems of similar complexity.
A decrease in the birth rate is not the only cause of a declining number of school pupils. Besides, internal migration may cause a substantial drop in the rural population. In such cases, the number of pupils in rural schools will decline, resulting in underutilization of such schools, while at the same time, new schools must be built in urban areas to accommodate the children of those who have migrated to the cities. Thus, planning for an increased number of pupils in some areas may take place simultaneously with planning for decreased numbers in other areas within the same region/country.
This decline in natality, combined with a remarkable increase in human life spans leads to a number of imbalances, and in particular to a high proportion of retired people with respect to the active population.
Some developing countries, considering that their populations were growing too quickly, have applied a policy of birth control. In others, increased education of girls, urbanization, and the gradual liberation of women have brought about a sharp drop in natality without the need for a restrictive policy; all that was needed was adequate information and easy access to methods of contraception.
This was the case in such Asian countries as Taiwan, Singapore, the Republic of Korea and Thailand. In India, the Philippines and Iran, the fertility rate has fallen gradually but remains high. In Pakistan, where Islam is the dominant influence, the fertility rate remained stable at a high level (6.5-7 children per woman on average) until 1985.
Measures of Mortality
The study of mortality deals with effects of death on population. A distinction can usually be made between two types of mortality, depending on the cause of death: endogenous mortality and exogenous mortality. Endogenous mortality means death occurring from a cause which is to some extent inherent in the individual. Thus, when a child is born with deformities and dies because of these deformities, the death of that child can be declared endogenous.
Deaths due to old age, or the diseases which accompany old age, can also be classified under this category. Exogenous mortality, on the contrary, refers to deaths from other causes, such as accidents, contagious diseases, and dietary deficiencies. Although this may appear to be a very clear-cut distinction, it is much less clear in practice, either because the causes of death may be unknown or not declared, or because there may be multiple causes of death. However, the distinction can nonetheless prove very useful.
Although the progress of hygiene and medical care on the one hand, and the rise in living standards on the other, are capable of reducing exogenous mortality to a marked extent, they have very little effect on endogenous mortality. The fact is that although medical progress can prevent certain premature deaths, it cannot prolong life beyond a certain limit.
Methods of measuring mortality
The calculation of mortality rates requires detailed statistical data, notably including statistics for the number of survivors in a cohort at a given age and the number of deaths at the same age for the same cohort. In many cases, however, such detailed statistics are not available, so instead of calculating mortality rates at different ages, demographers settle for calculating death rates, which give the number of deaths at a given age during a calendar year as a ratio of the total population of that age during the same year.
Crude Death Rate (CDR)
The simplest way of measuring mortality is the crude death rate. CDR is the ratio of the total registered deaths of a specified year to the total mid-year population multiplied by 1000. It thus resembles the crude birth rate discussed above.
D
CDR = —— X 1000
P
D = Total number of deaths registered during the calendar year
(Jan. 1 – Dec. 31)
F = Total population at the middle of the year (i.e., on July 1)
This rate is quite straightforward to calculate and does not require detailed mortality statistics. However, it has the same drawbacks as the crude birth rate where international comparisons are concerned. As an example, over the 1990-1995 period the crude death rate in Syria was 5.6 per thousand, while that of the United Kingdom was 9.4 per thousand.
These figures give the misleading impression that the mortality level was higher in the United Kingdom than in Syria. This apparent paradox is easily explained by the fact that mortality varies greatly with age: it is low among younger people and, of course, higher for more advanced ages. The proportion of deaths in relation to the total population, therefore, depends on the age structure of that population. A youthful population such as that of Syria (i.e. a population in which the proportion of younger people is larger than that of older people) will have fewer deaths and hence a lower crude death rate than an older population.
The general nature of the crude death rate thus diminishes its significance to demographers, who – faced with the fact that the level of mortality varies substantially according to age – are inclined to calculate age-specific mortality rates. These rates obviously provide much more accurate indications of the level of mortality in a given population. Even, mortality rates are calculated separately for men and for women as they also differ between the sexes. Most countries display excess male mortality, i.e. the mortality rate is higher for men than for women at advanced ages.
Age-specific mortality rates
To calculate mortality rates by age, demographers generally use the concept of the ‘cohort’, which refers to all the people born during the same calendar year. The number of individuals in a cohort decreases over time, owing to deaths. Thus, one can study the effects of mortality by following the change in the size of a cohort over time.
Infant Mortality Rate (IMR)
In mortality studies, special attention should be given to infant mortality, because the mortality level of very young children is relatively high. The infant mortality level is of particular interest to educational planners because this level determines the number of children for whom schooling must be provided in the future. Infants are defined as an exact age group namely ‘ ZERO’ or those children in the first year of life, who have not yet reached age one.
-Infant mortality is measured by the mortality rate at age 0, that is, the ratio of deaths from birth to 1 year of age to the total number of live births in the generation. Still-births are not included in infant mortality, and this distinction can be carried even further, bringing us to the concept of perinatal mortality.
do
IMR = ——- X 1000
B
Where do = Number of deaths below age one, registered during calendar year
B = Number of live births, registered during the same year
The infant mortality rate is specifically important in the analysis of mortality because infant deaths account for a substantial number of all deaths, especially in those countries where health conditions are poor. We have already discussed the differences between endogenous and exogenous mortality, pointing out that endogenous mortality in the case of infants relates to those who are born alive but considered as being doomed to a very short existence in the present state of medical knowledge. Perinatal mortality is therefore obtained by adding endogenous mortality to still-births. Finally, there are two overlapping concepts:
Perinatal mortality = Still-births + Endogenous mortality
Infant mortality = Endogenous mortality + Exogenous mortality
While the concepts of perinatal mortality and infant mortality are theoretically very accurate, it is often difficult to measure them accurately, and the distinctions made above remain theoretical rather than practical, even in countries where civil registration procedures are well organized.
Alternative Methods of Measuring Population Growth
The rate of natural population growth is easily calculated and convenient to use, but it is derived from the crude birth rate and crude death rate, and thus has the same drawbacks as these rates: it does not take account of the age structure, and thus does not allow meaningful comparisons between countries. For this reason, the concept of ‘reproduction’ may be substituted for the concept of population growth.
The idea here is to find out whether the current generation is capable of quantitatively replacing the preceding generation which gave birth to it. If we follow a generation from birth to the point where it has completed the procreation of all its descendants, and if we then compare the number of these descendants with the number of persons in the original generation, we obtain a measurement of the ‘replacement’ of one generation by another.
This forms the basis for calculating the reproduction rate. In general, however, instead of comparing the total number of descendants with the total number in the generation to which they were born, demographers compare the number of female births with the number of women in the generation. It should be noted that, in general, more boys are born than girls, and that the relative male birth rate is about 1.05. In other words, out of every 1,000 births, there are approximately 512 boys and 488 girls (512/488 = 1.05). The crude reproduction rate is therefore equal to the average number of female babies born to each woman of the generation considered.
As discussed earlier, the crude death rate is not easily interpreted. The fact that this rate is stable does not mean that mortality has diminished. In reality, the decline in mortality observed through a comparison of death rates by age is offset by the ageing of the population.
To obtain a more complete and accurate view of reproduction, however, we must take into account not only the fertility, but also the mortality of women. Some women die before reaching child-bearing age (15 years) or during the child-bearing period (15-49). For this reason, a net reproduction rate is calculated, which takes into consideration both the fertility and the mortality of women.
In principle, the reproduction rate is a generation rate. In order to calculate this, it would be necessary to follow a cohort of women born 50 years ago, and count the total number of female babies to whom they gave birth. What is important, however, is not the past trend in fertility, but its current characteristics. For this reason, instead of computing actual generation rates, current rates are used.
In studying the future trend of a population, the net reproduction rate is undoubtedly more useful than the crude rate of natural growth, which merely expresses the current balance between births and deaths. A decline in the birth rate may well be masked by a declining death rate, with results in the births-to-deaths balance remaining positive. But natality may decline to such a level that the generations no longer replace themselves. The population becomes older (increase in the proportion of old people), and after a certain lapse of time it declines (decrease in total number of people).
Preparing population projections
There are two main reasons for making population projections. The first is scientific curiosity, which can lead one to investigate, for example, what would be the trend and structure of a population if certain demographic parameters were to change.
An attempt can be made, for instance, to discover the consequences for a given population of a gradual decline in infant mortality over the next 20 years. Projections of this kind are sometimes called conditional projections, because they show what would occur if such and such a condition were fulfilled, without attempting to determine the most probable future situation. In this sense, such forecasts can never be mistaken! Nevertheless, they can be very useful and instructive, as they provide a means of detecting the indirect consequences of certain possible population changes. The second concern is of much greater practical usefulness.
In this case, an attempt is made to forecast future population growth. Starting with the current situation, particularly the current structure of the population by sex and age and the current level of mortality and fertility, the basic aim is to forecast what this level will be in the near future. This leads to the estimation of projective rates. Using these projective rates, it is possible to calculate the number of survivors and then to complete the picture by making a forecast or projection of births.
(a) Calculation of survivors
The calculation of survivors is one of the most reliable aspects of population projection, since this calculation deals with cohorts which are already born; the only assumptions which have to be made concern mortality. If the death rate at the earliest ages (0-4 years) is excluded, the death rate among young people (5-20 years) is low and the risk of error is not very high.
For that reason, short-term school enrolment forecasts and projections for the active population are relatively accurate. In discussing mortality, we spoke of the mortality rate and the death rate. But it is evident that instead of considering the number of deaths, one can take the number of survivors: for example, one can calculate the proportion of individuals of the same cohort, at a given age, who are still living one year later. This gives us what is known as a survival rate.
If out of the 420,000 children 1 year old in a given cohort, 2,100 die before reaching the age of 2, the survival rate at 1 year is: (420,000 – 2,100)/420,000 = 0.995.
Instead of calculating the survival rate at a given age, one can compute the survival rate for a whole age group. One can determine, for example, the proportion of children in the 0-4 year group who, five years later, will constitute the 5-9 year group.
On the basis of current survival rates and the probable mortality trend in the near future, one can estimate projective survival rates. As the mortality level is not the same for men and women, one must compute these rates separately for each sex. In this connection, the model life tables compiled by the demographic staff of the United Nations can again be of some use.
These tables offer the advantage of describing the various levels of mortality (corresponding to increasingly higher life expectancy at birth). Hence, if no other means are available for estimating projective survival rates and if a certain decline in mortality is nevertheless expected, the survival rates corresponding to a slightly lower mortality level can be used as projective rates. Once the projective rates have been determined, one need only apply them to the current population figures by age or by age group in order to arrive at an estimation of the age structure in future years.
(b) Birth projections
Whereas the calculation of survivors is made on the basis of the current population structure by sex and the mortality level, birth projections are based on the age structure of the female population (in particular women of child-bearing age) and the fertility level.
It should be noted that while the mortality rates at the younger ages are low (which reduces the possibility of numerical errors in estimating survivors), fertility rates at these ages are not low, and hence the results of birth projections are not as accurate as those of survivor calculations. This is especially true when there is a sudden and unexpected variation in fertility. The first step in making birth projections is to calculate projective fertility rates.
This can be done by taking current fertility data and making various assumptions as to the future trend. The next step is to estimate the number of women in the various cohorts.
Forecasting school enrolments
Forecasting future school enrolments involves two distinct stages. The purpose of such a forecast may be to estimate total educational costs, and hence the funding required. In this case, the enrolment figures with which one is concerned are the overall figures for the country. When it concerns implementing an educational plan, however, it is necessary to know also how these school enrolments are distributed over the country’s territory. This involves forecasting on the local scale.
(a) On the national scale
Firstly, one needs to estimate the school-age population. This can be done on the basis of the number of births. On the basis of the number of births observed, it is possible to estimate the numbers of children of primary school age (6-11) and lower secondary school age (12-14. Up to the end of compulsory schooling, the forecasting of school enrolment figures presents no particular difficulties, as the number of children enrolled in school is approximately equal to the school-age population.
But at the other educational levels, only a part of the school-age population will have access to education. In theory, this proportion depends on both social demand (i.e. the desire for education expressed by pupils and parents) and the policy established by the government. In practice, however, things are not quite so simple.
Even the most authoritarian governments are obliged to take social demand into account when setting policy. By the same token, all governments, no matter how liberal, seek to influence that social demand. In the end, therefore, it is the combined action of these two factors that determines the level of educational enrolment rates. Where the sole aim is to satisfy social demand, it is necessary to estimate how this demand will change in the future. In this case, the study of past trends may be instructive: on the basis of the observed levels of the enrolment rate in the past, extrapolation gives us the probable level of this rate in the future.
If, however, educational development is regarded as a priority – in other words, if an effort is to be made to facilitate such development to the greatest possible extent (anticipating, and to some extent encouraging, social demand) – then school enrolment rates become targets to be met. For example, it might be decided to raise the enrolment rate gradually in order to achieve universal compulsory education within a given number of years.
As stated above, however, the implementation of an educational plan requires more than forecasting the overall numbers for a country; it is also necessary to try to see how these numbers will be distributed throughout the country. Thus, after forecasting the number of enrolments on a national scale, it is necessary to make similar forecasts on the local scale.
(b) On the local scale
In forecasting at the local level, it is of course necessary to take into account migration. In general, international migration has little effect on the school-age population, except in cases of civil war, such as in Liberia, Sierra Leone and Afghanistan. Internal igration, however, may have a strong impact on the school-age population.
These migratory movements are sometimes very large. Increases in the populations of towns and cities are due as much to internal population movements as to the natural growth of the population, if not more so. Unfortunately, very little is known about such internal migration. In most cases, no accurate data are available as to the origin or the age of migrants, and even the size of these migratory movements is measured only from time to time when population censuses are taken.
It is thus understandable that any forecasts concerning internal migration will be very approximate. However, in any event, there are three kinds of internal migration: (1) movements from one part of the country to another; (2) movements from rural areas towards urban areas close by; and (3) movements away from the centres of urban areas towards the surrounding areas.
Movements from the centre of large towns or cities towards the surrounding areas are observed mostly in the developed countries, but movements from rural areas towards towns and cities (urbanization) are now a feature of all countries, developed and developing, and it is these movements that have the greatest effect on educational development. Since the factors which may affect such internal population movements are mostly to be found at the local level (the extent to which towns and cities attract inflows from the surrounding areas, the flow of people towards areas where development is most rapid, etc.), it is the local authorities who are most familiar with them.
Local authorities are also the best informed of the specific educational problems of the region or area, past educational enrolment levels, etc. For all these reasons, they are in the best position to forecast future numbers of students on the local scale. Many errors could be avoided by involving local authorities as closely as possible in the formulation of educational plans.
Conclusion
In this module, an attempt has been made to show the effects that demographic factors may have on educational development. It has also been indicated how population data may be used in the preparation of an educational plan.
However, a number of topics could not be addressed in detail. For example, demographic techniques have been mentioned in a very cursory fashion as the purpose of this module is not to analyse demographic techniques in detail; they have been discussed only to the extent to which they help show how population data are collected, the assumptions which must sometimes be made for lack of sufficiently detailed data, the adjustments which must be made in order to correct any discernible errors, and so on.
In countries where statistics are reliable, where censuses are taken regularly and carefully, and vital statistics units operate efficiently, population data are presented with all the necessary accuracy and precision, and the demographic projections based on such data have every chance of being accurate as well – although there is always the possibility of error in the event of abrupt changes in population behaviour. In other countries, however, and especially the developing countries, planners do not have such accurate data and must take precautions in using whatever statistics are available.
Population data are nevertheless crucial to educational planning. No meaningful planning is possible without reference to the current and future demographic profile of the country. If that profile is known with only some degree of accuracy, it is essential to be sufficiently flexible in the determination of educational targets to allow adjustments to be made should more accurate data later become available.
References
Attané, I. 2000. “La fécondité chinoise à l’aube du XXIe siècle”. In: Population, 55(2), March-April 2000, 237.
Bertrand, O. 1992. Planning human resources: methods, experiences and practices (Fundamentals of educational planning, 41). Paris: UNESCO/IIEP.
Caillods, F. 1983. School mapping and microplanning. Paris: UNESCO/IIEP.
Carron, G.; Châu, T.N. 1981. Regional disparities in educational development. Paris: UNESCO/IIEP.
Châu, T.N. 1972. Population growth and cost of education in developing countries. Paris: UNESCO/IIEP.
Châu, T.N. 1996. Viet Nam: performance of the educational sector. World Bank internal document.
Coale, A.J.; Demery, P. 1966. Regional model life tables and stable populations. Princeton, N.J.: Princeton University Press.
Demographic Yearbook. 1998. New York: United Nations.
Dietsch, B.; Malègue, C.; Migeon, M. 2000. “Les enseignants à l’aube de l’an 2000”. In: Éducation et Formations, 56, June 2000. Paris: Ministry of Education.
Egerö, B.; Hammarskjöld, M.; Munck, L. 2000. AIDS, the challenge of this century: prevention, care and impact mitigation. Stockholm: SIDA.
Hallak, J. 1977. Planning the location of schools: an instrument of educational policy. Paris: UNESCO/IIEP.
Harbison, F. 1967. Educational planning and human resource development (Fundamentals of educational planning, No. 3). Paris: UNESCO/IIEP.
Human development report. 1996-. Paris: UNDP, Economica.
Hunter, S.; Williamson, J. 2000. Children on the brink: updated estimates and recommendations for intervention. Washington: USAID.
International Labour Office (ILO). 1991. International standard classification of occupations, revised edition (ISCO-88). Geneva: ILO.
International Labour Office (ILO). 1993. Fifteenth international conference of labour statisticians, conference report. ICLS/15/
D.6 (Rev. 1). Geneva: ILO.
INED (Institut national d’études démographiques). N.d. Web site www.ined.fr.
Jones, G. 1975. Population growth and educational planning in developing nations. New York: John Wiley and Sons.
Johnstone, J.N. 1982. “Three useful but often forgotten education system indicators”. In: Socio-economic Planning Sciences, 16(4). London.
Kelly, M.J. 2000. Planning for education in the context of HIV/ AIDS (Fundamentals of educational planning, 66). Paris: UNESCO/IIEP.
Liu, B.A. 1966. Estimating future school enrolment in developing countries: a manual of methodology. New York: UNESCO/United Nations.
Ministry of Education, France. 2000. Éducation et Formations, 55, January-March 2000. Paris: Ministry of Education.
Ministry of Education, Tunisia. 1998. Annuaire statistique 1998. Tunis: Ministry of Education.
Muhsam, H.V. (Ed.). 1975. Education and population: mutual impacts. Dolhain: Ordina Edition.
Nizard, A. 2000. “Les effets sur la mortalité de quelques maux contemporains : sida, hépatite, alcool et tabac”. In: Population, 55(3), May-June 2000.
Pressat, R. 1961. L’analyse démographique : méthodes, résultats, applications. Paris: Presses Universitaires de France.
Preston, S.H. 1976. Mortality patterns in national populations. New York: Academic Press.
Reed, L.; Merell, M. 1939. “A short method for constructing an abridged life table”. In: American Journal of Hygiene, 30(2), September 1939.
UNAIDS. 1997. Report on the global HIV/AIDS epidemic. Geneva: UNAIDS.
UNAIDS. 2000. AIDS epidemic update, December 1999. New York: UNAIDS.
UNESCO. 2001. UNESCO’s strategy for HIV/AIDS preventive education. Paris: UNESCO/IIEP.
United Nations. 1957. Methods of appraisal of quality of basic data for population estimates (Population studies, 23, ST/SOA/Series A). New York: United Nations.
United Nations. 1982. Model life tables for developing countries. New York: United Nations.
United Nations. 1990a. International standard industrial classification. Statistical papers, Series M, No. 4, Rev. 3. New York: United Nations.
United Nations. 1990b. Additional principles and recommendations for population and housing censuses. Doc. ST/ESA/STAT/SER. M/67/Add. 14. New York: United Nations.
United Nations. 1999. World Population Prospect, the 1998 revision, Vol. I: Comprehensive Tables. New York: United Nations.
United Nations. 2001. HIV/AIDS: population impact and policies 2001. New York: United Nations.
US Census Bureau. 2001. Estimates and projections prepared for the report, ‘Global Population Profile: 2000’. Washington: US Census Bureau.
Yearbook of Labour Statistics. 2000. Geneva: International Labour Office.
Youdi, R.V.; Hinchliffe, K. (Eds.). 1985. Forecasting skilled manpower needs: the experience of eleven countries. Paris: UNESCO/IIEP.